The equity risk premium is the excess return an investor is compensated for minus the risk-free rate (six-month US Treasury). Looking at BRKB returns we will use statistical testing to drive further insights on the equity risk premium affecting trailing returns.
First, we can look at whether the distribution of returns is statistically different from two time periods from 1996–2010 to 2011-current using the KS-test. The results show that we get a p-value of .057 which is almost statistically significant at the 5% level.
Next, we can test if our data is heteroskedastic, which occurs when looking at the relationship between the equity risk premium and the returns. This means when our x and y variables increase the distance between data points gets more spread out.
When conducting the Breuch Pagen test we get a p-value of .693 from 1996–2011 and a p-value of .66 from 2012-current. This tells us there is no heteroskedasticity in the earlier period, and no heteroskedasticity currently, confirming what we see from our graphs.
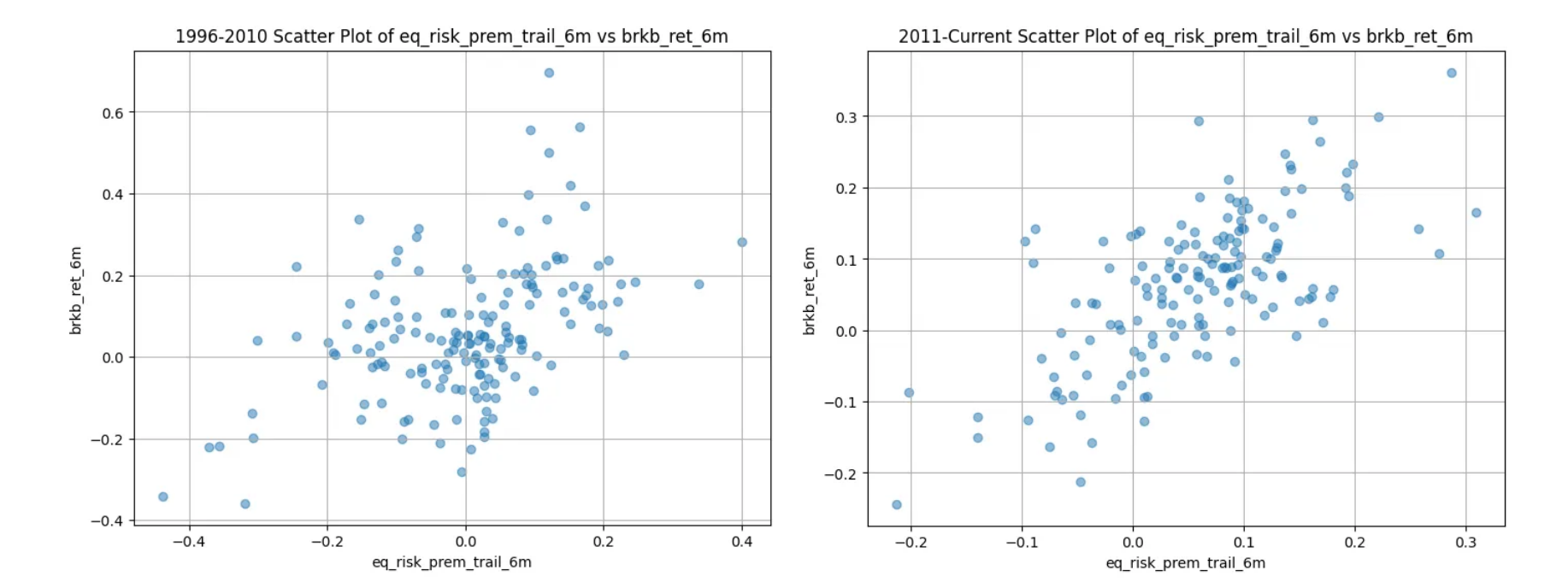
Next, we can run the Chow test to see if there is a structural change in the relationship between returns and the equity risk premium giving us a p-value of .005. Since this below a critical value of .01, we can reject the null hypothesis and conclude that there is a structural break in our data. The relationship between the trailing equity risk premium and trailing returns is significantly different from 1996–2010 and 2011-currently.
From our statistical tests, heteroskedasticity was not present in both periods. We concluded that the returns from 1996–2010 and 2011-currently are borderline statistically significant at the 5% level. The results from our Chow test confirmed that there has been a structural change in the relationship between the 6m-trailing equity risk premium and the 6m-trailing returns for BRKB.
Code can be found here
https://github.com/Gaiden-Spence/Equtiy-Risk-Premium-Analysis
This article should never be considered as investing guidance or advice in any capacity whatsoever. It is solely intended to help readers discover intriguing theories about markets that they may or may not want to explore on their own.
These are my own opinions and do not represent the opinions of my employer in any capacity whatsoever.